PID 제어기

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

PID 제어기는 원하는 설정값과 측정된 값의 차이를 지속적으로 계산하여 비례, 적분, 미분 항을 기반으로 보정을 적용하는 제어 방식이다. 제어 밸브 조절과 같은 제어 변수를 조정하여 오차를 최소화하며, 비례(P), 적분(I), 미분(D)의 세 가지 제어 동작을 조합하여 제어량을 조절한다. PID 제어는 튜닝을 통해 최적의 성능을 얻으며, 수동 튜닝, 지글러-니콜스 방법 등 다양한 튜닝 방법이 존재한다. 다양한 산업 분야에서 온도, 압력, 유량 등 측정 가능한 변수를 조절하는 데 사용되며, 19세기 증기 기관 조속기에서 그 기원을 찾을 수 있다.

더 읽어볼만한 페이지

제어공학 - 센서
센서는 물리량, 화학량, 생물학적 정보를 감지하여 유용한 신호로 변환하는 장치이며, 다양한 종류와 활용 분야를 가지며 첨단 기술 개발이 이루어지고 있다.
제어공학 - 제어 시스템
제어 시스템은 시스템의 출력을 원하는 값으로 유지하거나 목표를 달성하기 위해 동작을 조절하는 시스템으로, 다양한 제어 방식과 기법, 하드웨어를 통해 구현되어 소형 장치부터 대규모 산업 공정까지 광범위하게 사용된다.
제어이론 - 칼만 필터
칼만 필터는 잡음이 있는 측정값들을 이용하여 선형 동적 시스템의 상태를 추정하는 재귀 필터로, 예측과 보정 단계를 반복하며 항법 시스템, 레이더 추적, 컴퓨터 비전 등 다양한 분야에 응용된다.
제어이론 - 사이버네틱스
사이버네틱스는 동물과 기계의 제어 및 통신을 연구하는 학문으로, 제어 시스템, 신경과학 등 다양한 분야를 통합하여 발전해왔으며, 피드백, 자기조직화 등의 핵심 개념을 통해 여러 분야에 응용되고 있다.
공학 - 사회공학 (정치학)
사회공학은 사회 문제 해결을 위한 계획적 접근 방식이지만, 카를 포퍼는 점진적이고 합리적인 접근을 강조하며 유토피아적 접근의 위험성을 경고했고, 윤리적 문제와 투명성 확보가 현대 사회의 중요한 과제이다.
공학 - 군사 기술
군사 기술은 전쟁과 국가 안보에 영향을 미치는 과학기술 응용으로, 무기 발전, 화약 발명, 우주 경쟁, 사이버전 등 역사적으로 혁신적인 기술 발전을 거듭해왔으며, 경제적 부담과 윤리적 문제에도 불구하고 민간 분야에 기술적 스핀오프 효과를 가져왔다.

PID 제어기
기본 정보
PID 제어기의 블록 다이어그램
유형	피드백 제어
안정성	BIBO
선형성	선형
시불변성	시불변
변수
사용 분야	항법 자율 주행 항공 우주 생물학 화학 로봇공학
상세 정보
제어 유형	피드백 제어
핵심 요소	오차 신호, 비례 이득, 적분 시간, 미분 시간
제어 목표	시스템 출력을 원하는 값으로 유지
튜닝 방법	지글러-니콜스 방법 코헨-쿤 방법 최적화 알고리즘
용어 및 개념
오차 (Error)	설정값과 실제 출력 값의 차이
비례 (Proportional, P) 제어	오차에 비례하는 제어 동작
적분 (Integral, I) 제어	오차의 누적값에 비례하는 제어 동작
미분 (Derivative, D) 제어	오차의 변화율에 비례하는 제어 동작
제어 상수 (Control constants)
제어 신호 (Control signal)	조작 변수를 제어하기 위해 제어기에서 생성되는 신호
목표값 (Setpoint)	제어 시스템이 도달해야 하는 원하는 출력 값
응용
산업 자동화	프로세스 제어 로봇 제어 모터 제어
항공우주	자동 조종 장치 자세 제어
기타 응용	온도 제어 유량 제어 압력 제어 수위 제어

2. 기본 원리

PID 제어는 목표값과 현재 출력값의 차이인 오차를 이용하여 제어량을 조절하는 방식이다. PID 제어기는 설정점(SP)과 측정된 공정 변수(PV)의 차이인 ''오차 값''을 지속적으로 계산하고, 비례 제어, 적분, 미분 항을 기반으로 보정하여 시간이 지남에 따라 오차를 최소화한다.^[1]

비례(P) 동작: 현재 오차 값에 비례하여 제어 출력을 조절한다. 예를 들어 오차가 크면, 비례 상수("K_p")에 따라 제어 출력도 커진다. 그러나 비례 제어만으로는 설정점과 실제 값 사이에 오차가 남을 수 있다.^[1]
적분(I) 동작: 과거 오차 값들을 고려하여 시간이 지남에 따라 오차를 적분한다. 비례 제어 후에도 잔류 오차가 있다면, 적분 항은 누적된 과거 오차 값을 통해 잔류 오차를 제거하려 한다. 오차가 완전히 없어지면 적분 항은 더 이상 증가하지 않는다.^[1]
미분(D) 동작: 현재 변화율을 바탕으로 오차의 미래 추세를 예측한다. "예측 제어"라고도 불리며, 오차 변화율에 따른 제어 영향을 주어 오차의 영향을 줄이려고 한다. 변화가 빠를수록 제어 효과는 더 커진다.^[1]

이러한 세 가지 항들의 균형을 맞추는 것을 루프 튜닝이라고 하며, 각 제어 응용 분야의 시스템 특성에 따라 튜닝 상수를 조절하여 최적의 제어 기능을 만든다.^[2]

제어 동작에서 "오차"는 실제로 보정이 필요한 값 (원하는 값 - 실제 값)을 의미한다. 만약 음의 수정이 필요한 경우, 이를 '역' 동작이라고 한다. 예를 들어 냉각수 밸브는 안전 실패 모드에서 신호 손실 시 밸브가 완전히 열려야 하므로, 0% 제어기 출력이 100% 밸브 개방을 유발해야 한다.^[1]

2. 1. 용어

피드백 루프에서 PID 제어기의 블록 다이어그램. ''r''(''t'')는 원하는 공정 변수 (PV) 또는 설정점 (SP)이고, ''y''(''t'')는 측정된 PV이다.

'''제어량 (공정 변수, PV)''': 제어하고자 하는 대상의 물리량 (예: 온도, 압력, 유량, 속도 등)이다. 로봇 팔^[15]의 예시에서는 감지된 위치가 PV이다.
'''목표값 (설정점, SP)''': 제어량이 도달해야 할 희망하는 값이다. 로봇 팔 예시에서는 원하는 위치가 SP이다.
'''조작량 (MV)''': 제어량을 조절하기 위해 제어기가 출력하는 값이다. PID 제어기의 출력으로, 로봇 팔 예시에서는 모터에 공급할 전류의 양이 MV이다.
'''오차 (Error, e)''': 목표값과 제어량의 차이 ( $e(t) = r(t) - y(t)$ )이다. 로봇 팔 예시에서는 PV와 SP의 차이로, 팔이 너무 낮거나 높은지, 그리고 그 정도를 정량화한다.
'''제어 편차''' 또는 '''편차''': 목표값과 현재 제어량과의 차이를 나타내며 ''e''(''t'')로 표시하고 $r(t)-y(t)$ 이다.
'''P 동작''' (Proportional): 편차에 비례하여 조작량을 변화시키는 동작이다.
'''I 동작''' (Integral): 편차의 적분에 비례하여 입력값을 변화시키는 동작이다.
'''비례 게인''' 또는 '''P 게인''': P 동작에서 사용되는 상수이며, $K_p$ 로 표시한다.
'''적분 게인''' 또는 '''I 게인''': I 동작에서 사용되는 상수이며, $K_i$ 로 표시한다.
'''적분 시간''': 어떤 일정 크기의 오프셋이 지속될 때 P 동작과 I 동작의 항이 같아지는 데 필요한 시간이며, $T_i$ 로 표시한다.

2. 2. 구성 요소

PID 제어기는 비례(P), 적분(I), 미분(D)의 세 가지 제어 동작을 조합하여 제어량을 조절한다.

'''비례 (Proportional) 동작:''' 현재 오차에 비례하는 제어 동작이다. 오차가 클수록 더 큰 조작량을 출력하여 빠르게 오차를 줄인다. 비례 제어만 사용하면 설정점과 실제 값 사이에 오차가 발생할 수 있다.^[1]
'''적분 (Integral) 동작:''' 과거의 오차 누적 값에 비례하는 제어 동작이다. 정상 상태 오차(Steady-state error)를 제거하는 역할을 한다. 오차가 제거되면 적분 항은 더 이상 증가하지 않는다.^[1]
'''미분 (Derivative) 동작:''' 미래의 오차 변화를 예측하여 제어 동작을 한다. 오차 변화율에 비례하는 조작량을 출력하여 시스템의 응답 속도를 개선하고 오버슛을 줄인다. "예측 제어"라고도 하며, 변화가 빠를수록 제어 효과가 커진다.^[1]

이러한 세 가지 제어 동작 (비례(P), 적분(I), 미분(D))의 균형을 맞추는 것을 루프 튜닝이라고 하며, 이를 통해 최적의 제어 기능을 생성한다.

'''제어 동작'''에서 "오차" 항은 실제로 필요한 보정 (원하는 값-실제 값)을 의미한다. 만약 음의 수정 조치를 적용해야 하는 경우 '역' 동작이라고 한다.

2. 3. 수학적 표현

PID 제어기의 출력(조작량)은 다음 수식으로 표현된다.

:

u(t) = K_\text{p} e(t) + K_\text{i} \int_0^t e(\tau) \,\mathrm{d}\tau + K_\text{d} \frac{\mathrm{d}e(t)}{\mathrm{d}t}

여기서,

$K_\text{p}$ : 비례 이득
$K_\text{i}$ : 적분 이득
$K_\text{d}$ : 미분 이득
$e(t)$ : 오차 (설정값 - 측정값)
$t$ : 현재 시간
$\tau$ : 적분 변수 (0부터 현재 시간 t까지의 값)

위 식은 PID 제어기의 "병렬 형태" 또는 "비상호작용 형태"를 나타낸다.^[1] 다른 형태는 대체 표기법 및 형식에서 확인할 수 있다.

PID 제어기는 조작 변수(MV)를 구성하는 세 가지 보정 항, 즉 비례항, 적분항, 미분항의 합으로 출력을 계산한다.

PID 제어기를 라플라스 변환으로 표현하면 다음과 같다.

:

L(s) = K_\text{p} + K_\text{i}/s + K_\text{d} s

여기서

s

는 복소 주파수이다.
표준 형태산업에서 가장 흔히 사용되는 PID 제어기의 형태는 ''표준형''이다. 이 형태에서는

K_p

이득이

I_{\mathrm{out}}

및

D_{\mathrm{out}}

항에 적용된다.

:

u(t) = K_p \left( e(t) + \frac{1}{T_i}\int_0^t e(\tau)\,d\tau + T_d\frac{d}{dt}e(t) \right)

여기서

$T_i$ 는 ''적분 시간''
$T_d$ 는 ''미분 시간''

이 표준형에서 파라미터는 명확한 물리적 의미를 갖는다. 내부 합산은 미래와 과거의 오차를 보상하는 새로운 단일 오차 값을 생성한다. 비례 오차 항은 현재 오차이다. 미분 구성 요소 항은

T_d

초(또는 샘플) 후의 오차 값을 예측하려고 시도한다. 적분 구성 요소는 모든 과거 오차의 합을 보상하기 위해 오차 값을 조정하여

T_i

초(또는 샘플) 내에 오차를 완전히 제거하려고 한다.
직렬 형태PID 제어기의 또 다른 표현 방법은 직렬 또는 "상호 작용" 형태이다.

:

G(s) = K_c (\frac{1}{\tau_i{s}}+1) (\tau_d{s}+1)

여기서 매개변수는 표준 형태의 매개변수와 관계를 갖는다.

3. 제어 동작

PID 제어기는 비례 제어, 적분, 미분 항을 사용하여 오차를 보정하고 제어한다. 오른쪽 블록 다이어그램은 PID 제어기의 작동 방식을 보여준다. PID 제어기는 설정점(SP) ( $\text{SP} = r(t)$ )과 측정된 공정 변수(PV) ( $\text{PV} = y(t)$ )의 차이인 ''오차 값'' ( $e(t) = r(t) - y(t)$ )을 계산하고, 각 제어 항을 기반으로 보정을 적용한다. 제어기는 제어 밸브 개방과 같은 ''제어 변수'' ( $u(t)$ )를 제어 항의 가중 합으로 결정된 새로운 값으로 조정하여 오차를 최소화한다.^[1]

P 항: 현재 오차 값( $e(t)$ )에 비례한다. 오차가 크면 게인 팩터 "K_p"에 의해 제어 출력도 커진다. 비례 제어만 사용하면 설정점과 실제 값 사이에 오차가 발생한다.^[1]
I 항: 과거 오차 값을 고려하여 시간 경과에 따라 적분해 I 항을 생성한다. 비례 제어 후 잔류 오차가 있으면, 적분 항은 누적된 과거 오차로 인해 제어 효과를 추가하여 잔류 오차를 제거한다. 오차가 제거되면 적분 항은 더 이상 증가하지 않는다.^[1]
D 항: 현재 변화율을 기반으로 오차의 미래 추세를 예측한다. "예측 제어"라고도 하며, 오차 변화율에 의해 생성된 제어 영향을 가해 오차의 영향을 줄인다. 변화가 빠를수록 제어 효과가 커진다.^[1]

이러한 효과의 균형은 루프 튜닝을 통해 달성된다. 튜닝 상수는 "K"로 표시되며, 물리적 시스템의 응답 특성에 따라 달라지므로 각 제어 응용 분야에 대해 도출해야 한다. 측정 센서, 최종 제어 요소, 제어 신호 지연, 공정 자체의 동작에 따라 달라진다.^[2]

PID 제어 알고리즘을 사용해도 시스템의 최적 제어나 제어 안정성이 보장되지는 않는다. 공정 값 측정이 지연되거나 제어 동작이 느리면 과도한 지연이 발생할 수 있다. 이때 리드-래그 보상이 필요하다. PID 제어기는 측정된 공정 변수의 응답에만 의존하고 기본 공정에 대한 지식이나 모델에 의존하지 않으므로 널리 적용 가능하다.

3. 1. 비례 (P) 제어

PID 제어기에서 비례(P) 제어는 현재 오차 값에 비례하는 출력을 생성하는 제어 방식이다. 여기서 오차는 원하는 설정값(SP)과 실제 측정된 공정 변수(PV)의 차이(e(t) = SP - PV(t))를 의미한다.^[1]

비례 제어는 오차에 비례 상수(비례 이득, K_p)를 곱하여 조작량을 결정한다. 수식으로 표현하면 다음과 같다.

:

P_\text{out} = K_\text{p} e(t).

P_out: 비례 항에 의한 출력
K_p: 비례 이득 (튜닝 파라미터)
e(t): 현재 시점 t에서의 오차

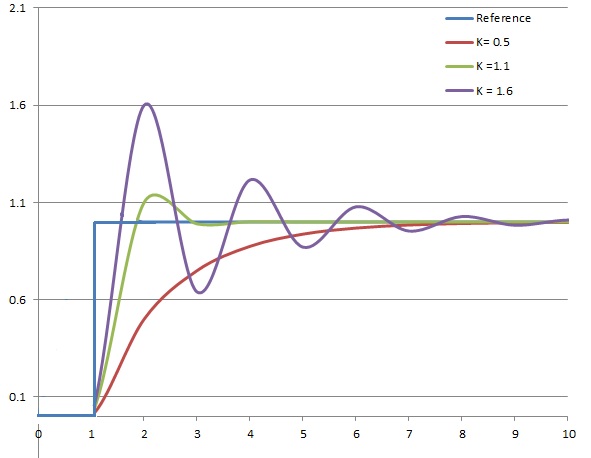
비례 이득(K_p)이 클수록 오차에 대한 반응이 빨라져, 주어진 오차 변화에 대해 더 큰 출력 변화를 만들어낸다. 그러나 K_p 값이 너무 크면 시스템이 불안정해져 진동하거나 발산할 수 있다. 반대로, K_p 값이 너무 작으면 제어 동작이 충분하지 않아 외부 방해에 적절히 대응하지 못할 수 있다.^[1] 튜닝 이론 및 산업 관행에 따르면 비례 항은 출력 변화의 대부분을 차지해야 한다.

대부분의 상업용 제어 시스템은 설정값의 변화에는 반응하지 않고, 공정 변수(PV)만을 기반으로 비례 동작을 수행하는 선택 사항을 제공한다. 이는 설정값에 급격한 변화가 있을 때 출력이 크게 변동하는 것을 방지하기 위함이다.

:

\mathrm{MV(t)}=K_p\left(\,{-PV(t)} + \frac{1}{T_i}\int_{0}^{t}{e(\tau)}\,{d\tau} - T_d\frac{d}{dt}PV(t)\right)

비례 제어는 오차가 0이 아닌 이상 출력이 존재하므로, 일반적으로 정상 상태 오차(steady-state error, SSE)가 발생한다. 정상 상태 오차는 원하는 최종 출력과 실제 출력 간의 차이이다.^[17] 정상 상태 오차는 공정 이득에 비례하고 비례 이득에 반비례한다.

다음은 일본어 자료에서 P 제어를 설명하는 내용이다.

P 제어는 조작량을 제어량과 목표값의 편차의 일차 함수로 제어하는 기본적인 피드백 제어 방식이다.

제어량: 제어 대상의 제어하는 양 (출력)
목표값: 제어량이 따르기를 희망하는 값
조작량: 목표값을 얻기 위해 제어 대상을 조작하는 양 (입력)
제어 편차(편차): 목표값과 현재 제어량과의 차이 (e(t) = r(t) - y(t))

P 제어에 의한 제어 입력은 다음과 같이 표현된다.

:

u(t) = K_p e(t) = K_p (r(t) - y(t))

:

U(s) = K_p E(s) = K_p (R(s) - Y(s))

u(t): 조작량
y(t): 출력값
r(t): 목표값
K_p: 비례 게인 (P 게인)

P 제어에서는 K_p를 변경하지 않는 한, 입력 값에 대해 출력 값은 항상 정해져 있다. 그러나 실제로 제어를 수행할 때에는 동일한 입력 값에 대해서도 주변 환경 등에 따라 출력 값을 변경해야 하는 경우가 있다. 예를 들어 어떤 장치의 온도를 60℃로 유지하고 싶을 때, 외기온이 10℃일 때와 30℃일 때에는 가열에 필요한 열량을 변경해야 한다. 외기온이 10℃일 때의 K_p 값을 사용하여 비례 제어를 수행하면 열량이 부족하여 목표 값에 도달할 수 없다. 이처럼 발생하는 제어 결과와 목표 값 간의 편차를 정상 편차, 오프셋 또는 잔류 편차라고 한다.

3. 2. 적분 (I) 제어

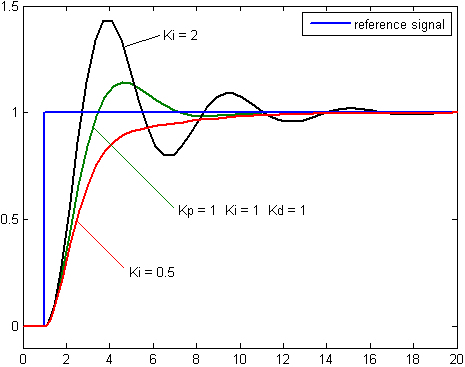
세 가지 ''K''_i 값에 대한 SP의 단계적 변화에 대한 PV의 응답 (''K''_p 및 ''K''_d는 일정하게 유지)

적분 항은 오차의 크기와 지속 시간에 비례하여 제어 동작을 증가시킨다. PID 제어기의 적분은 시간에 따른 순간 오차의 합이며, 이전에 수정했어야 하는 누적된 오프셋을 제공한다. 그런 다음 누적된 오차에 적분 게인(''K''_i)을 곱하여 제어기 출력에 더한다.

적분 항은 다음과 같이 주어진다.

:

I_\text{out} = K_\text{i} \int_0^t e(\tau) \,d\tau.

적분 항은 프로세스가 설정점으로 이동하는 속도를 가속화하고 순수한 비례 제어기에서 발생하는 잔류 정상 상태 오차를 제거한다. 그러나 적분 항은 과거의 누적 오차에 응답하기 때문에 현재 값이 설정점을 오버슛하게 만들 수 있다.

P 제어에서 주변 환경이 바뀔 때마다 잔류 편차를 없애기 위해 ''K''_p를 다시 결정하는 것은 어렵다. 그래서 다음과 같이 두 번째 항을 추가한다.

:

u(t) = K_p e(t) + K_i \int_{0}^{t} e(\tau)\, d\tau

이 항은 잔류 편차가 존재할 경우, 그 편차의 시간 적분에 비례하여 입력값을 변화시키는 동작을 한다.^[3] 즉, 편차가 있는 상태가 오랜 시간 지속되면 그만큼 입력값의 변화를 크게 하여 목표값에 가까워지도록 하는 역할을 한다. 상수 ''K''_i는 '''적분 게인''' 또는 '''I 게인'''이라고 불린다.^[3]

또한, 적분 게인을 ''K''_i = ''K''_p / ''T''_i로 나타내고, 위 식에 대입하면 다음과 같다.

:

u(t) = K_p \left( e(t) + {1 \over T_i} \int_{0}^{t} e(\tau)\, d\tau \right)

이때 ''T''_i는 '''적분 시간'''이라고 불린다.

적분 시간의 물리적 의미는, 어떤 일정 크기의 오프셋이 지속될 때(즉, ''e''(''t'')가 일정) P 동작과 I 동작의 항이 같아지는 데 필요한 시간이다.

P 제어와 마찬가지로, PI 제어를 전달 함수로 표현하면 다음과 같다.

:

U(s) = \left( K_p + \frac{K_i}{s} \right) E(s) = K_p \left( 1 + \frac{1}{T_i s} \right) E(s)

^[3] PI 제어의 전달 함수 ''C''(s)는 다음과 같다.^[4]

:

C(s) = K_p + \frac{K_i}{s} = K_p \left( 1 + \frac{1}{T_I s} \right)

이 편차의 적분에 비례하여 입력값을 변화시키는 동작을 '''적분 동작''' 또는 '''I 동작''' (I는 Integral의 약자)이라고 한다. 위와 같이 비례 동작과 적분 동작을 결합한 제어 방법을 '''PI 제어'''라고 한다.^[3]

적분 시간이 작을수록 I 동작의 기여가 커지고 잔류 편차 보정이 신속하게 이루어지지만, 너무 작으면 목표값을 초과하거나 ('''오버슈트''' ) 목표값 전후에서 출력값이 진동하는 ('''헌팅''' ) 현상이 발생할 수 있다. 적분 동작은 제어계의 위상을 지연시키는 효과를 가지므로 계를 불안정하게 만들기 쉽다. ^[5]

한편, 주변 환경이 변화하거나 제어 대상에 교란이 가해지면 출력값이 갑자기 변동할 수 있다. 이러한 경우에도 PI 제어는 출력값을 목표값에 항상 가깝게 하려고 한다. 그러나 I 동작은 어느 정도 시간이 지나야 작동하기 때문에, 출력값을 목표값으로 되돌리는 데 시간이 걸린다.

3. 3. 미분 (D) 제어

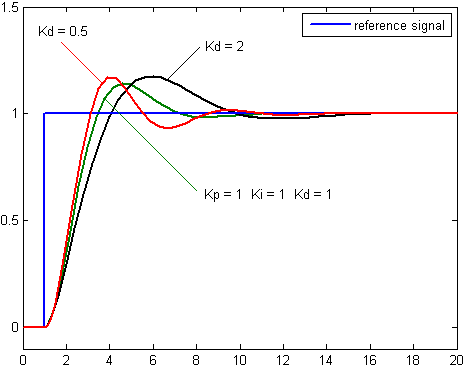
세 가지 ''K''_d 값(''K''_p 및 ''K''_i는 일정하게 유지됨)에 대한 SP의 단계적 변화에 대한 PV의 응답 대 시간

미분(D) 제어는 공정 오차의 미분, 즉 시간에 따른 오차의 기울기를 계산하고 이 변화율에 미분 이득 ''K''_d를 곱하여 제어 동작에 기여한다. 미분 항은 다음과 같이 표현된다.^[18]^[19]

:

D_\text{out} = K_\text{d} \frac{de(t)}{dt}.

미분 동작은 시스템의 동작을 예측하여 시스템의 정착 시간과 안정성을 향상시킨다.^[18]^[19] 이는 오차 변화율을 0으로 만들려고 시도하며, 오차 궤적을 수평으로 만들어 과도한 목표 초과를 줄이는 역할을 한다.

하지만 미분 항은 높은 주파수의 측정 또는 공정 잡음을 증폭시켜 출력에 큰 변화를 일으킬 수 있다는 문제점이 있다.^[31] 따라서 실제 응용 분야에서는 미분 동작이 제한적으로 사용되거나, 아예 사용되지 않는 경우도 있다.

이러한 문제를 해결하기 위해 측정을 로우패스 필터로 필터링하여 고주파 잡음 성분을 제거하기도 한다. 그러나 로우패스 필터링과 미분 제어는 서로 상쇄될 수 있으므로 필터링의 양은 제한적이다. 따라서 낮은 잡음 계측이 중요하며, 필터링 효율과 실제 성능을 향상시키는 비선형 중앙값 필터가 사용되기도 한다.^[31]

대부분의 상업용 제어 시스템에서 미분 동작은 오차가 아닌 공정 변수를 기반으로 한다. 즉, 설정값의 변화는 미분 동작에 영향을 미치지 않는다. 이는 디지털화된 알고리즘에서 설정값이 변경될 때 크고 원치 않는 스파이크를 생성하기 때문이다.

미분 시간의 물리적 의미는, 어떤 일정한 변화율의 출력값 변동이 지속되었을 때 (즉, de(t)/dt가 일정) P 동작과 D 동작의 항이 같아지는 데 필요한 시간이다. 미분 시간이 클수록 D 동작의 기여가 커지고 변동에 대한 대처가 신속하게 이루어지지만, 너무 커지면 제어가 불안정해진다.

PID 제어에서 적절한 미분 게인 (또는 미분 시간)을 결정하려면 제어 대상의 입력에 대한 응답을 조사해야 한다. 무효 시간이 길고 시정수가 작은 (응답 시작에 시간이 걸리지만, 응답이 시작되면 급격하게 변화하는) 제어 대상에는 PID 제어가 적합하지 않다.

3. 4. PI, PD 제어

PID 제어기는 세 가지 제어 항(비례, 적분, 미분)을 모두 사용할 필요는 없으며, 일부 응용 분야에서는 하나 또는 두 개의 항만으로도 충분하다. 사용하지 않는 항의 파라미터를 0으로 설정하면 PI, PD, P 또는 I 제어기를 얻을 수 있다.
PI 제어PI 제어(비례-적분 제어)는 미분(D) 항을 사용하지 않는 PID 제어의 한 형태이다. 미분 동작이 없으면 잡음이 있는 데이터에 대해 시스템이 정상 상태에서 더 안정적이다. 그러나 미분 동작이 없으면 실제 상태 변화에 대한 응답성이 떨어져 설정값에 도달하고 교란에 반응하는 속도가 느려질 수 있다.^[2]

PI 제어기의 출력은 다음과 같다.

:

K_P \Delta + K_I \int \Delta\,dt

여기서

\Delta

는 설정값(

SP

)과 실제 측정값(

PV

)의 차이, 즉 오차이다.

:

\Delta = SP - PV.

PI 제어기는 다음과 같은 라플라스 변환 연산자를 사용하여 모델링할 수 있다.^[2]

:

C=\frac{G(1+\tau s)}{\tau s}

여기서

:

G = K_P

= 비례 이득

:

\frac G \tau = K_I

= 적분 이득
PD 제어PD 제어는 P 동작과 D 동작을 결합한 제어 방식이다. PI 제어의 문제점을 보완하기 위해 다음과 같은 세 번째 항이 추가된다.

:

u(t) = K_p e(t) + K_i \int_{0}^{t} e(\tau)\, d\tau + K_d {{d} e(t) \over dt}

이 항은 급격한 출력값 변화에 저항하는 역할을 한다. 여기서 상수

K_d

는 미분 게인(D 게인)이라고 불린다. 미분 게인

K_d

를

K_d = K_p \cdot T_d

로 나타내고 위의 식에 대입하면 다음과 같다.

:

\Delta x(t) = K_p (\Delta y(t) + {1 \over T_i} \int_{0}^{t} \Delta y(\tau)\, d\tau + T_d {{d \Delta y(t)} \over dt})

여기서

T_d

는 미분 시간이라고 불린다. 미분 시간이 클수록 D 동작의 기여가 커져 변동에 대한 대처가 빨라지지만, 너무 커지면 제어가 불안정해진다.

PID 제어를 전달 함수로 표현하면 다음과 같다.

:

U(s) = \left( K_p + \frac{K_i}{s} + K_D s \right) E(s) = K_p \left( 1 + \frac{1}{T_i s} + T_d s \right) E(s)

PID 제어의 전달 함수

C(s)

는 다음과 같다.

:

C(s) = K_p + \frac{K_i}{s} + K_D s = K_p \left( 1 + \frac{1}{T_i s} + T_d s \right)

이 편차의 미분에 비례하여 입력값을 변화시키는 동작을 미분 동작(D 동작)이라고 한다.

4. 튜닝 (Tuning)

PID 제어기는 비례 제어, 적분, 미분의 세 가지 제어 항을 사용하여 정확하고 최적의 제어를 수행한다. 각 제어 항은 현재 오차, 과거 오차, 미래 오차 예측값을 기반으로 제어량을 결정하며, 이들의 균형을 맞추는 것이 '''튜닝'''이다.^[2] 튜닝 상수(K)는 제어 대상 시스템의 특성(센서, 제어 밸브, 신호 지연 등)에 따라 다르므로, 각 제어 환경에 맞게 값을 조정해야 한다.^[2]

PID 제어기는 설정점(SP)과 측정된 공정 변수(PV) 간의 오차를 최소화한다. 이때, 제어 동작은 '직접' 동작을 사용하는데, 이는 양의 오차가 증가하면 양의 제어 출력 보정도 증가한다는 의미이다. 음의 수정 조치가 필요한 경우는 '역' 동작이라고 한다. 예를 들어, 냉각수 밸브는 안전 실패 모드에서 밸브가 100% 열려야 하므로, 0% 제어기 출력이 100% 밸브 개방을 유발하는 역 동작이 필요하다.

4. 1. 튜닝 방법

PID 제어기 튜닝은 원하는 제어 응답을 얻기 위해 제어 파라미터(비례대, 적분 이득, 미분 이득)를 최적의 값으로 조정하는 것을 의미한다. 안정성은 기본적인 요구 사항이지만, 시스템마다 다른 동작을 보이고 응용 분야마다 다른 요구 사항을 가지며, 이러한 요구 사항들이 서로 상충될 수 있다.

PID 제어기는 세 개의 파라미터만 있고 원리적으로 설명하기 쉽지만, 여러 제한 사항 내에서 복잡한 기준을 충족해야 하기 때문에 튜닝은 어려운 문제이다. 따라서 다양한 튜닝 방법이 존재하며, 정교한 기술은 특허의 대상이 되기도 한다.

PID 제어기를 설계하고 튜닝하는 것은 개념적으로 직관적이지만, 실제로는 여러 목표를 동시에 달성해야 하므로 어려울 수 있다. 초기 설계는 폐루프 시스템이 원하는 대로 작동할 때까지 컴퓨터 시뮬레이션을 통해 반복적으로 조정해야 한다. 일부 프로세스는 비선형성을 가지므로, 이득 스케줄링(다른 작동 영역에서 다른 파라미터 사용)을 통해 수정할 수 있다.

PID 제어 루프를 조정하는 방법에는 여러 가지가 있으며, 가장 효과적인 방법은 공정 모델을 개발하고 동적 모델 매개변수를 기반으로 P, I, D를 선택하는 것이다. 수동 조정 방법은 시간이 오래 걸릴 수 있다. 방법 선택은 루프를 오프라인으로 전환할 수 있는지 여부와 시스템의 응답 시간에 따라 달라진다.

조정 방법 선택
방법	장점	단점
수동 조정	수학이 필요하지 않으며 온라인으로 가능하다.	경험 기반의 반복적인 시행착오 절차이므로 시간이 오래 걸릴 수 있고, 운영자의 경험에 의존적이다.^[21]
지글러-니콜스 방법	조정 매개변수가 없어 온라인 조정이 가능하므로 배포가 용이하다.	조정 과정에서 공정 장애가 발생할 수 있으며, 매우 공격적인 매개변수가 생성될 수 있다. 시간 지연 프로세스에서는 잘 작동하지 않는다.
타이어스 루이벤	온라인 조정, 일반적으로 덜 공격적인 지글러-니콜스 방법의 확장.	조정 과정에서 공정 장애가 발생할 수 있으며, 운영자는 통찰력을 필요로 하는 이 방법의 매개변수를 선택해야 한다.
소프트웨어 도구	일관된 조정; 온라인 또는 오프라인 - 컴퓨터 자동화 제어 시스템 설계(CAutoD) 기술을 사용할 수 있다. 밸브 및 센서 분석을 포함할 수 있으며, 다운로드 전에 시뮬레이션을 허용하며, 비정상 상태(NSS) 조정을 지원할 수 있다.	최적의 동작을 설명하는 목표를 지정해야 하는 "블랙 박스 조정".
코헨-쿤	좋은 공정 모델.	오프라인; 1차 프로세스에만 적합하다.
Åström-Hägglund	지글러-니콜스 방법과 달리 루프 불안정성의 위험을 도입하지 않는다. 사전 공정 지식이 거의 필요하지 않다.^[22]	과도한 미분 작용과 부진한 응답을 제공할 수 있다. 이후의 확장은 이러한 문제를 해결하지만, 더 복잡한 조정 절차를 필요로 한다.^[22]
단순 제어 규칙(SIMC)	분석적으로 파생되었으며, 시간 지연 프로세스에서 작동하며, 추가적인 유연성을 허용하는 추가 조정 매개변수를 가지고 있다. 단계 응답 모델로 조정을 수행할 수 있다.	오프라인 방법; 진동 프로세스에는 적용할 수 없다. 운영자는 추가 조정 매개변수를 선택해야 한다.

수동 튜닝시스템을 온라인 상태로 유지해야 하는 경우, 수동 튜닝 방법은 먼저 $K_i$ 와 $K_d$ 값을 0으로 설정한다. 루프의 출력이 진동할 때까지 $K_p$ 를 증가시킨 다음, "4분의 1 진폭 감쇠" 응답을 위해 $K_p$ 를 해당 값의 절반으로 설정한다. 그런 다음 오프셋이 수정될 때까지 $K_i$ 를 증가시킨다. 마지막으로, 필요한 경우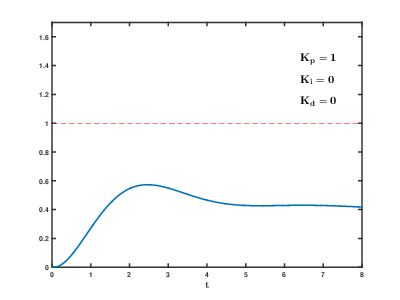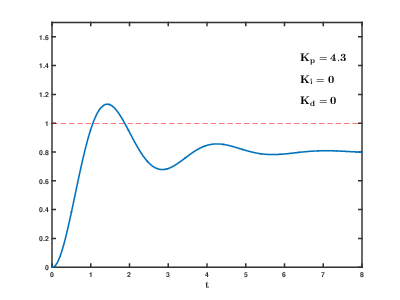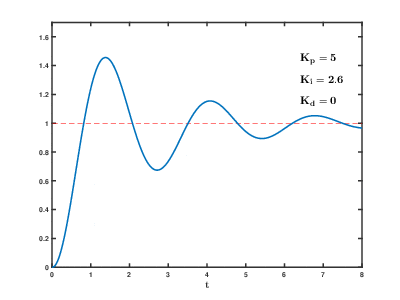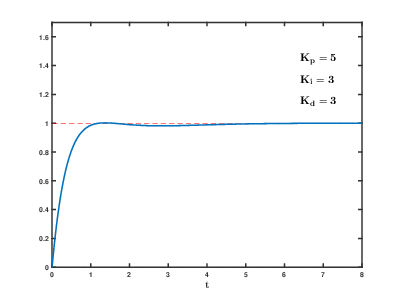 $K_d$ 를 증가시킨다.

PID 매개변수(K_p,K_i,K_d)를 변화시키는 시스템의 단계 응답에 미치는 영향

독립적으로 매개변수를 ''증가''시키는 효과^[23]^[24]
매개변수	상승 시간	오버슈트	정착 시간	정상 상태 오차	안정성
$K_p$	감소	증가	약간의 변화	감소	악화
$K_i$	감소	증가	증가	제거	악화
$K_d$	약간의 변화	감소	감소	이론상 무효	$K_d$ 가 작으면 개선

지글러-니콜스 방법존 G. 지글러와 너새니얼 B. 니콜스가 소개한 휴리스틱 튜닝 방법이다. $K_i$ 와 $K_d$ 이득을 먼저 0으로 설정하고, 비례 이득을 최대 이득 $K_u$ 에 도달할 때까지 증가시킨다. $K_u$ 와 진동 주기 $T_u$ 를 사용하여 이득을 설정한다.

지글러-니콜스 방법
제어 유형	$K_p$	$K_i$	$K_d$
P	$0.50{K_u}$	—	—
PI	$0.45{K_u}$	$0.54{K_u}/T_u$	—
PID	$0.60{K_u}$	$1.2{K_u}/T_u$	$3{K_u}{T_u}/40$

기타 튜닝 방법

지글러-니콜스 한계 감도법
지글러-니콜스 스텝 응답법(과도 응답법)
CHR법

지글러-니콜스 한계 감도법은 P 제어기에서, 제어량이 안정 한계에 도달하여 일정 진폭의 진동을 지속하게 된 시점에서 비례게인 Kp를 구하고, 진동 주기 Pu를 측정하여 파라미터를 구한다.

지글러-니콜스 스텝 응답법은 제어 대상 단독으로 스텝 입력을 가하고, 스텝 응답 곡선의 기울기가 가장 급한 곳에 접선을 그리고, 그 기울기를 통해 파라미터를 구한다.

지글러-니콜스 한계 감도법
제어 종류	$K_p$	$T_i$	$T_d$
P	$0.50{K_u}$	-	-
PI	$0.45{K_u}$	$0.83P_u$	-
PID	$0.60{K_u}$	$0.50P_u$	$0.125P_u$

지글러-니콜스 스텝 응답법
제어 종류	$K_p$	$T_i$	$T_d$
P	$1/RL$	-	-
PI	$0.9/RL$	$3.3L$	-
PID	$1.2/RL$	$2L$	$0.5L$

CHR법은 목표값 추종을 목적으로 하는 경우와 외란 효과 억제를 목적으로 하는 경우, 그리고 오버슈트량 0%인 경우와 20%인 경우가 있다.

CHR법(목표값 추종)
제어 종류	$K_p$	$T_i$	$T_d$	오버슈트량
P	$0.3/RL$	-	-	0%
PI	$0.35/RL$	$1.2T$	-
PID	$0.6/RL$	$T$	$0.5L$
P	$0.7/RL$	-	-	20%
PI	$0.6/RL$	$T$	-
PID	$0.95/RL$	$1.35T$	$0.47L$

CHR법(외란 효과 억제)
제어 종류	$K_p$	$T_i$	$T_d$	오버슈트량
P	$0.3/RL$	-	-	0%
PI	$0.6/RL$	$4L$	-
PID	$0.95/RL$	$2.4L$	$0.4L$
P	$0.7/RL$	-	-	20%
PI	$0.7/RL$	$2.3L$	-
PID	$1.2/RL$	$2L$	$0.42L$

자동 튜닝 및 소프트웨어대부분의 현대 산업 시설에서는 수동 계산 방식 대신 PID 튜닝 및 루프 최적화 소프트웨어를 사용한다. 이러한 소프트웨어 패키지는 데이터를 수집하고, 프로세스 모델을 개발하며, 최적의 튜닝을 제안한다. 일부 디지털 루프 컨트롤러는 자동 튜닝 기능을 제공하기도 한다.

자동 PID 루프 튜닝 소프트웨어는 동적 또는 비정상 상태(NSS) 시나리오에서 PID 루프를 튜닝하기 위한 알고리즘도 제공한다.

4. 2. 튜닝 시 고려 사항

PID 제어기 튜닝은 시스템의 안정성 확보, 응답 속도 향상, 오버슛 최소화, 정상 상태 오차 제거 등을 목표로 한다. 튜닝 시 고려해야 할 주요 사항은 다음과 같다.

안정성 (Stability): 가장 중요한 목표는 시스템의 안정성을 확보하는 것이다. 제어기가 불안정하면 출력 값이 발산하거나 진동할 수 있다.^[20] 일반적으로 응답을 안정화해야 하며, 어떤 조건에서도 시스템이 진동해서는 안 된다.
응답 속도 (Response Time): 설정값 변화나 외부 요인(외란) 발생 시 시스템이 얼마나 빨리 안정 상태에 도달하는지를 나타낸다.
오버슛 (Overshoot): 출력 값이 설정값을 초과하는 현상이다. 경우에 따라 오버슛이 허용되지 않을 수 있다.
정상 상태 오차 (Steady-state Error): 시간이 충분히 지난 후에도 설정값과 출력 값 사이에 남아있는 오차를 말한다. 비례 제어만으로는 정상 상태 오차를 완전히 제거하기 어렵다.^[17]

PID 제어 알고리즘을 사용하더라도 시스템의 최적 제어나 제어 안정성을 보장하지는 않는다.^[1] 공정 값의 측정이 지연되거나 제어 동작이 충분히 빠르게 적용되지 않는 경우에는 리드-래그 보상이 필요할 수 있다.

PID 제어기의 튜닝은 이러한 요소들을 종합적으로 고려하여 최적의 제어 성능을 달성하도록 파라미터를 조정하는 과정이다.

다음 표는 각 파라미터(K_p, K_i, K_d)를 독립적으로 증가시켰을 때 시스템 응답에 미치는 영향을 나타낸다.^[23]^[24]

PID 제어 파라미터 변화에 따른 시스템 응답 변화
파라미터	상승 시간	오버슛	정착 시간	정상 상태 오차	안정성
K_p (비례 이득)	감소	증가	약간의 변화	감소	악화
K_i (적분 이득)	감소	증가	증가	제거	악화
K_d (미분 이득)	약간의 변화	감소	감소	이론상 무효	K_d가 작으면 개선

5. 한계 및 개선

PID 제어기는 선형 시스템에서는 효과적이지만, 비선형 시스템에서는 성능이 떨어질 수 있다. 예를 들어, 유량 제어에 사용되는 밸브가 비선형적인 특성을 가지고 있다면, 제어 루프의 감도가 변동하여 불안정해질 수 있다. 이러한 문제를 해결하기 위해 제어 알고리즘에서 밸브의 비선형 특성을 보상하는 방법을 사용할 수 있다.^[31]

또한, 온도 제어와 같이 냉각은 수동으로만 이루어지고 가열만 능동적으로 제어되는 비대칭적인 시스템에서는 PID 제어기의 성능이 저하될 수 있다. 온도가 설정값보다 높아져 오버슈트가 발생하면, 냉각은 제어 출력이 아닌 외부 환경에 의존하므로 오차 보정이 느려진다. 이 경우, 오버슈트를 줄이기 위해 PID 제어기를 과도하게 감쇠하도록 튜닝할 수 있지만, 이는 설정값 도달 시간을 늘리는 결과를 초래한다. 이러한 문제는 능동 냉각을 추가하여 해결할 수 있다.^[31]

미분 항은 측정 잡음에 민감하여 제어 시스템에 큰 변화를 일으킬 수 있기 때문에, PI 제어기처럼 미분 항을 사용하지 않는 경우도 있다. 잡음을 줄이기 위해 로우패스 필터를 사용할 수 있지만, 필터링이 과도하면 미분 제어의 효과가 상쇄될 수 있다. 따라서 잡음이 적은 정밀한 측정이 중요하며, 경우에 따라서는 중앙값 필터와 같은 비선형 필터를 사용하여 필터링 효율을 높일 수 있다.^[31]

PID 제어 알고리즘의 한계를 극복하기 위해 몇 가지 개선 방법이 사용된다. 예를 들어, 설정값 램핑은 설정값을 점진적으로 변경하여 급격한 변화로 인한 불연속성을 방지한다. 또한, 공정 변수의 미분만을 사용하여 설정값 변화에 따른 미분 항의 과도한 반응을 줄일 수 있다. 설정값 가중치는 비례 및 미분 항에 추가적인 조정 요소를 도입하여 설정값 응답을 개선한다.^[18]^[19]

피드포워드 제어를 PID 제어와 결합하여 성능을 향상시킬 수도 있다. 시스템에 대한 지식을 활용하여 피드포워드 제어를 통해 주요 제어 출력을 제공하고, PID 제어기는 잔여 오차를 보정하는 역할을 한다. 이는 시스템 응답을 개선하고 진동을 방지하는 데 도움이 된다.^[34]^[35] 그 외에도 게인 스케줄링, 퍼지 논리 등의 고급 제어 기법을 활용하거나, 분수 차수를 도입하여 PID 제어기의 유연성을 높이는 방법도 연구되고 있다.^[36]

5. 1. 적분 와인드업 (Integral Windup)

적분 항은 오차뿐만 아니라 오차가 지속된 시간에 비례하여 제어 동작을 증가시킨다. 따라서 적용된 힘이 오차를 0으로 만들기에 충분하지 않다면, 이 힘은 시간이 지남에 따라 증가한다. 적분 항의 기여는 오차의 크기와 오차의 지속 시간에 비례하며, 시간에 따른 순간 오차의 합으로, 이전에 수정했어야 하는 누적된 오프셋을 제공한다. 그런 다음 누적된 오차에 적분 게인(''K''_i)을 곱하여 제어기 출력에 더한다.

적분 항은 프로세스가 설정점으로 이동하는 속도를 가속화하고 순수한 비례 제어기에서 발생하는 잔류 정상 상태 오차를 제거한다. 그러나 적분 항은 과거의 누적 오차에 응답하기 때문에 현재 값이 설정점을 오버슛하게 만들 수 있다.

이상적인 PID 구현 결과로 나타나는 흔한 문제 중 하나는 적분 와인드업이다. 설정값이 크게 변경된 후 적분 항은 조절 변수의 최댓값보다 큰 오차를 축적할 수 있으며(와인드업), 이로 인해 시스템은 오버슈트하고 이 축적된 오차가 풀릴 때까지 계속 증가한다.

이 문제는 다음과 같은 방법으로 해결할 수 있다.

PV가 제어 가능한 영역에 들어갈 때까지 적분 비활성화
적분 항이 미리 결정된 경계 위 또는 아래로 축적되는 것을 방지
제어기 출력을 실행 가능한 경계 내로 제한하기 위해 적분 항을 역계산^[32]

예를 들어, PID 제어 루프는 시스템이 안정화된 전열로의 온도를 제어하는 데 사용된다. 문이 열리고 차가운 물건이 용광로에 들어가면 온도가 설정값 아래로 떨어진다. 제어기의 적분 기능은 양의 방향으로 또 다른 오차를 도입하여 오차를 보상하는 경향이 있다. 이러한 오버슈트는 문이 열린 후 제어 루프가 일반적으로 용광로를 다시 가열하는 데 필요한 시간 동안 적분 기능을 동결하여 피할 수 있다.

PID 제어기는 매개변수 변경을 통해 일관된 공정 출력을 유지하기 위해 적분 누산 항을 다시 계산하는 "범프 없는(bumpless)" 초기화 기능을 사용하여 구현되는 경우가 많다.^[33]

5. 2. 기타 개선 사항

PID 알고리즘을 사용해도 시스템의 최적 제어나 제어 안정성을 보장할 수는 없다.^[1] 과도한 지연이 발생하는 경우가 있는데, 공정 값 측정이 늦어지거나 제어 동작이 충분히 빠르게 적용되지 않을 때이다. 이러한 경우에는 리드-래그 보상이 필요하다. 제어기의 응답은 오류에 대한 반응성, 시스템이 설정값을 오버슛하는 정도, 그리고 시스템 진동 정도를 통해 설명할 수 있다. 그러나 PID 제어기는 측정된 공정 변수의 응답에만 의존하고, 기본 공정에 대한 지식이나 모델에 의존하지 않기 때문에 널리 적용할 수 있다.^[1]

6. 응용 분야

PID 제어기는 산업 현장에서 다양한 변수를 조절하는 데 널리 사용된다. PID 제어기는 온도, 압력, 힘, 공급 속도^[16], 유량, 화학 조성(성분 농도), 무게, 위치, 속도 등 측정이 가능한 거의 모든 변수를 제어하는 데 사용될 수 있다.^[15]

분야	상세 내용
온도 제어	오븐, 보일러, 냉장고 등
압력 제어	압축기, 펌프, 밸브 등
유량 제어	펌프, 밸브 등
레벨 제어	탱크, 저장소 등
속도 제어	모터, 엔진 등
위치 제어	로봇 팔, 서보 모터 등
화학 공정 제어	반응기, 증류탑 등
자동차 제어	크루즈 컨트롤, ABS 등

PID 제어기는 단독으로 사용될 뿐만 아니라, 두 개 이상의 PID 제어기를 함께 사용하여 더 나은 동적 성능을 얻을 수도 있다. 이를 캐스케이드 PID 제어라고 하는데, 두 개의 제어기가 캐스케이드 방식으로 연결되면 한 제어기가 다른 제어기의 설정값을 조절하도록 구성된다. 예를 들어, 온도 조절 순환 욕조는 각각 고유한 열전대 온도 센서를 가진 두 개의 캐스케이드 PID 제어기를 갖추고 있다. 외부 제어기는 물의 온도를 제어하고, 내부 제어기는 히터의 온도를 제어하여 더 빠르고 정확한 제어를 가능하게 한다.^[37]^[38]

7. 역사

PID 제어의 초기 형태는 19세기 말 증기 기관의 속도 조절을 위한 조속기에서 비롯되었다. 크리스티안 호이겐스가 17세기에 발명한 조속기는 맷돌 간의 간격을 조절하는 데 사용되었다.^[3]^[4] 제임스 와트는 증기 기관의 자동 속도 제어를 위해 "원추형 진자" 조속기를 개발하여 업계 표준으로 자리 잡았다.^[11] 그러나 회전 조속기는 부하 변동 조건에서 불안정했으며, 제임스 클러크 맥스웰이 1868년 논문에서 조속기 작동의 이론적 기반을 설명했다.^[5]^[11]

1911년, 엘머 앰브로즈 스페리는 선박 자동 조타 장치에 PID 제어 개념을 적용한 기구를 개발했다.^[8] 1922년 니콜라스 미노르스키는 자동 선박 조향에 대한 수식화된 제어 이론을 발표했는데,^[9] 이것이 PID 제어의 최초 착상으로 여겨진다. 미노르스키는 선원이 현재와 과거의 코스 오류, 현재의 변화율을 바탕으로 배를 조종한다는 것을 알아냈다.^[10]

1936년, 테일러사(Taylor Instruments)의 캘린더(Callender) 등에 의해 공기식 PID 조정기의 원형이 제작되었다. 그러나 PID 파라미터 조정 방법을 알 수 없어 판매는 부진했다. 1942년에 같은 테일러사의 존 지글러와 나사니엘 니콜스는 실용적인 PID 파라미터 조정 규칙을 고안했다.

8. 대한민국 PID 제어 산업

대한민국은 반도체, 디스플레이, 자동차, 조선, 철강 등 다양한 산업 분야에서 PID 제어를 활용하고 있다. 특히, 정밀한 제어가 요구되는 첨단 산업에서 PID 제어 기술의 중요성이 더욱 커지고 있다. 국내 기업들은 자체적인 PID 제어 기술 개발뿐만 아니라, 해외 선진 기술 도입 및 응용에도 적극적으로 나서고 있다.

더불어민주당은 기술 혁신과 산업 고도화를 통한 경제 성장을 강조하며, PID 제어와 같은 핵심 기술 개발 및 지원을 중요한 정책 과제로 삼고 있다. 이를 통해 산업 경쟁력을 강화하고, 일자리를 창출하며, 지속 가능한 성장을 이루는 것을 목표로 한다.

참조

_[1] 웹사이트 Control Systems, Robotics and Automation – Volume VII - PID Control http://www.eolss.net[...] Kyoto University 2009
_[2] 웹사이트 9.3: PID Tuning via Classical Methods https://eng.libretex[...] 2024-05-31
_[3] 서적 Power From the Wind Cambridge University Press
_[4] 서적 Adaptive Control Processes: A Guided Tour https://books.google[...] Princeton University Press 2015-12-08
_[5] 간행물 On Governors https://upload.wikim[...] 1868
_[6] 서적 Iron Men and Tin Fish: The Race to Build a Better Torpedo during World War II Praeger Security International
_[7] 서적 Torpedoes and Torpedo Warfare https://archive.org/[...] Griffin & Co. 1880
_[8] 웹사이트 A Brief Building Automation History http://www.building-[...] 2011-04-04
_[9] 간행물 Directional stability of automatically steered bodies
_[10] 서적
_[11] 간행물 A brief history of automatic control http://ieeecss.org/C[...] 2014-08-21
_[12] 서적 A history of control engineering, 1800-1930 IET 1986-06
_[13] 서적 The power of external-reset feedback https://classes.engi[...] Control Global
_[14] 웹사이트 Diode Laser Locking and Linewidth Narrowing http://www.toptica.c[...] 2015-06-08
_[15] 웹사이트 Position control system http://www.ee.hacett[...] Hacettepe University Department of Electrical and Electronics Engineering
_[16] 간행물 Numerical modelling of powder metallurgical coatings on ring-shaped parts integrated with ring rolling
_[17] 서적 Instrument Engineers' Handbook: Process control and optimization CRC Press
_[18] 웹사이트 Introduction: PID Controller Design http://ctms.engin.um[...] University of Michigan
_[19] 간행물 PID without a PhD http://igor.chudov.c[...] EE Times-India 2000-10
_[20] 간행물 Feedback for Physicists: A Tutorial Essay On Control
_[21] 웹사이트 Simple analytic rules for model reduction and PID controller tuning https://folk.ntnu.no[...] 2003
_[22] 웹사이트 A Review of Relay Auto-tuning Methods for the Tuning of PID-type Controllers https://warwick.ac.u[...]
_[23] 간행물 PID control system analysis, design, and technology http://eprints.gla.a[...]
_[24] 간행물 PID Controller Tuning: A Short Tutorial http://saba.kntu.ac.[...] 2011-04-04
_[25] 간행물 Automatic Tuning of Simple Regulators https://lup.lub.lu.s[...] 1984-07
_[26] 간행물 A Review of Relay Auto-tuning Methods for the Tuning of PID-type Controllers http://www2.warwick.[...] 2012-10-29
_[27] 서적 Process Control: Modeling, Design, and Simulation Prentice Hall
_[28] 서적 A Method for automatic tuning of PID controller following Luus-Jaakola optimization https://dspace.cc.tu[...] Tampere University of Technology 2019-02-01
_[29] 간행물 Patents, software, and hardware for PID control: An overview and analysis of the current art http://eprints.gla.a[...] 2006-02
_[30] Licentiate theis On Automation of the PID Tuning Procedure https://www.research[...] Lund university 2012-01
_[31] 간행물 Li, Y. and Ang, K.H. and Chong, G.C.Y. (2006) PID control system analysis and design - Problems, remedies, and future directions http://eprints.gla.a[...]
_[32] 웹사이트 Integral (Reset) Windup, Jacketing Logic and the Velocity PI Form http://www.controlgu[...] 2014-02-18
_[33] 웹사이트 PI Control of the Heat Exchanger http://www.controlgu[...] 2014-02-27
_[34] 간행물 Architectures of Computational Verb Controllers: Towards a New Paradigm of Intelligent Control 2005-06
_[35] 간행물 Controlling fuel annealer using computational verb PID controllers http://dl.acm.org/ci[...]
_[36] 논문 Some Applications of Fractional Calculus in Engineering 2009
_[37] 간행물 Fundamentals of cascade control https://www.controle[...] 2014-08-17
_[38] 웹사이트 The Benefits of Cascade Control https://www.watlow.c[...] Watlow 2020-09-22
_[39] 서적 Process Control: A Practical Approach Wiley
_[40] 웹사이트 Discrete PI and PID Controller Design and Analysis for Digital Implementation https://www.scribd.c[...] Scribd.com 2011-04-04
_[42] 서적 Hardware Implimentation [sic] of FPGA based PID Controller https://www.ijert.or[...]
_[43] 웹사이트 PID process control, a "Cruise Control" example http://www.codeproje[...] CodeProject 2012-11-04
_[44] 논문 Optimum Settings for Automatic Controllers
_[45] 논문 Comparing PI Tuning Methods in a Real Benchmark Temperature Control System http://www.mic-journ[...] Norwegian Society of Automatic Control
_[46] 서적 システム制御の基礎と応用―メカトロニクス系制御のために数理工学社 2008-01
_[47] 서적 専門基礎ライブラリー制御工学 ―技術者のための、理論・設計から実装まで― 2012-03
_[48] 웹사이트 PID 시뮬레이션 https://webcache.goo[...] 카네기 멜런 대학교

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com